Bases en mathématiques pour le Tage Mage
Le Test du Tage Mage fait appel à des bases fondamentales en mathématiques. Si vous avez lu l'article Réussir la partie calcul du Tage Mage, vous avez compris à quel point il est important de maitriser les bases en mathématiques pour la préparation du Tage Mage. Vous trouverez dans cet article le mininum à connaître pour être plus à l'aise pendant cette épreuve.
Vos tables de multiplication
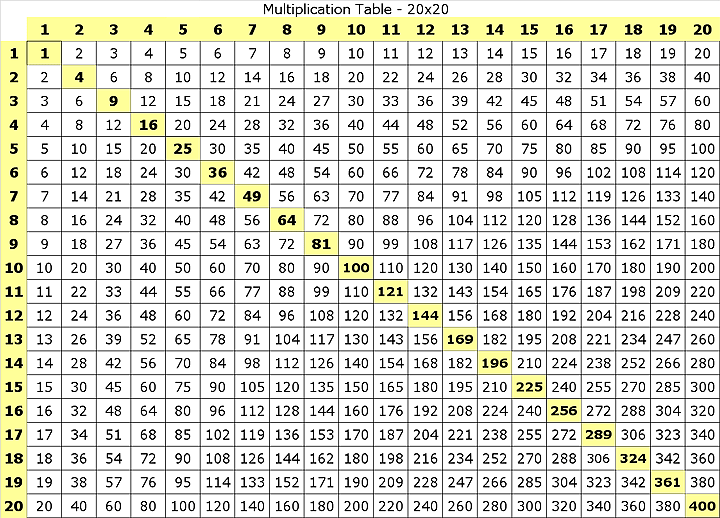
Les carrés et les cubes
| 1 | 1 CARRE | 1 CUBE |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 729 |
| 10 | 100 | 1000 |
| 11 | 121 | 1331 |
| 12 | 144 | |
| 13 | 169 | |
| 14 | 196 | |
| 15 | 225 | |
| 16 | 256 | |
| 17 | 289 | |
| 18 | 324 | |
| 19 | 361 | |
| 20 | 400 |
La géométrie de base
Périmètre
Rectangle : 2 ( Largeur + longueur )
Carré : 4L
Parallélogramme : 2 ( Longueur + largeur)
Cercle : 2.π.r
Aire
Triangle : (b.h) / 2
Rectangle : Largeur . Longueur
Losange : (diagonale 1.diagonale 2) / 2
Disque : π.r2
Cylindre : 2r . Longueur + 2 (π.r2)
Volume
Sphère : (4/3).π.r3
Cylindre : π.r2.h
Parallélépipède Rectangle : l.L.h
Cone : (π.r2.h)/3
Cube : c3
Quelques propriétés de géométrie
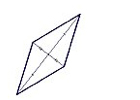
Losange :
- Les diagonales sont perpendiculaires et se coupent en leurs milieux.
Parallélogramme :
- Les diagonales se coupent en leurs milieux.
- Les cotés opposés sont parallèles.
- Les angles opposés sont égaux.
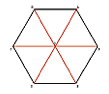
Hexagone régulier :
- La somme des angles est égale à 720°
- Il est composé de six triangles équilatéraux
Triangle :
- Rectangle, signifie que l'un des angles vaut 90°
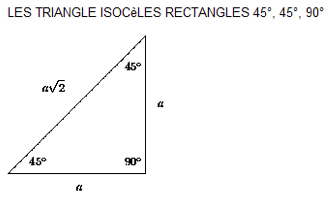
- Isocèle, signifie que deux des côtés ainsi que deux des angles du triangle sont égaux.
- Equilatéral, signifie que les trois côtés sont égaux ainsi que les angles qui font tous 60°
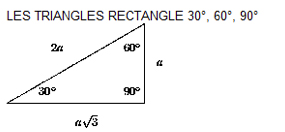
Les triangles d'angles 30°, 60°, 90° ont des longueurs de côtés proportionnelles. Par exemple, si le côté le plus court est égal à 5, alors l'hypothénuse est égal à 10 et le dernier côté 5 racine carrée de 3.
Pythagore
Si un triangle est rectangle, alors la somme des carrés des deux côtés est perpendiculaire et égale au carré de l’hypoténuse. Pour un triangle ABC, triangle rectangle en A : Alors BC2 = AB2 + AC2
Trois particularités à retenir :
- Les triangles rectangles de longueurs 3, 4 et 5 sont des triangles qui acceptent la règle de Pythagore.
- Les triangles rectangles de longueurs 5, 12, 13 sont aussi des triangles qui acceptent la règle de Pythagore.
- Les triangles dont les angles font respectivement 30°, 60°, 90°, la longueur du coté opposé à l’angle qui fait 30° est égal à la moitié de la longueur de l’hypoténuse.
Thalès
Soit un triangle ABC et deux points D et E, des droites (AB) et (AC) de sorte que la droite (DE) soit parallèle à la droite (BC).
Surface et Volume
- 1 are = 100 m2
- 1 hectare = 10 000 m2
- 1 m3 = 1000 litres
Des statistiques et probabilités
.jpg)
1/ tirage de p boules parmi n sans ordre et sans répétition :
Exemple : on tire deux cartes dans un jeu de 32, combien y a-t-il de tirage composé de 2 coeurs ? Réponse : il faut tirer 2 coeurs parmi les 8 présents dans le jeu, sans ordre et sans répétition.
2/ tirage de p boules parmi n avec ordre et sans répétition :
Exemple : une cours de chevaux se compose de 15 partants. Combien y a-t-il de tiercés possibles ? Réponse : il faut tirer (j'emploie ce verbe pour comparer avec le tirage de boules dans une urne) 3 chevaux parmi 15 avec ordre et sans répétition.
3/ tirage de p boules parmis n avec ordre et avec répétitions :
Exemple : un digicode se compose de 1à chiffres et de deux lettres/ Combien ya-t-il de codes composés de 4 "caractères" ? Réponse : il faut tirer 4 caractères parmi 12 avec ordre et avec répétitions.
Des notions sur les intérêts
î : intérêt K0 : capital de départ tps : temps Kn : capital + intérêt n : période
- les intérêts simples :
Cela signifie que l'argent placé ne va rapporter d'intérêts qu'une fois arrivé à la fin de sa période
î = K0 . tî . tps Kn = K0 . (1 + tî) . tps
- les intérêts composés :
Cela signifie que l'argent placé va rapporter des intérêts chaque année ou chaque mois et que ces intérêts supplémentaires vont générer à leurs tours des intérêts au temps t + 1
Kn = K0 . ( 1 + tî )n
Les nombres premiers
À connaitre ! Surtout les premiers…
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 et 97. Comment découpe-t-on un nombre en facteurs premiers ?
Réunir les multiples premiers d'un nombre.
Exemple : 550
550 peut s'écrire 55 x 10
55 x 10 = 11 x 5 x 5 x 2
11 x 5 x 5 x 2 = 550
Cette manière d'écrire est appelée "génétique du nombre», car vous ne pouvez trouver d'autres nombres entiers inférieurs aux nombres premiers 11, 5 ou 2.
Les puissances
- x0 = 1
- xa . xb =xa+b
- xa . ya = (x.y)a
- (xa)b = xa.b
- 1 / xa = x-a
- xa / xb = xa-b
Les critères de divisibilité
- Par 3 : La somme des chiffres du nombre doit être égale à un multiple de 3.
- Par 6 : La somme des chiffres du nombre doit être égale à un multiple de 3 ET de 2.
- Par 7 : Si le chiffre des dizaines du nombre moins deux fois le nombre des unités donne un multiple de 7 ; alors, Le nombre en question est un multiple de 7.
- Par 8 : Les trois derniers chiffres du nombre doivent être un multiple de 8.
- Par 11 : Si pour un nombre ABCD, AB + CD = multiple de 11 alors ; ABCD est un multiple de 11. Si pour un nombre ABC, A + BC = multiple de 11 ; alors, ABC est un multiple de 11.
- Par 13 : Si pour ABC, AB+4xC = multiple de 13 alors ABC est un multiple de 13.
Pair ou Impair ?
- Pair +/- Pair = Pair
- Pair+/- impair = Impair
- Impair +/-Impair = pair
- Pair . Pair = pair
- Pair . Impair = Pair
- Impair . Impair = Impair
- (Pair)N = pair
- (Impair)N =Impair
Les conversions
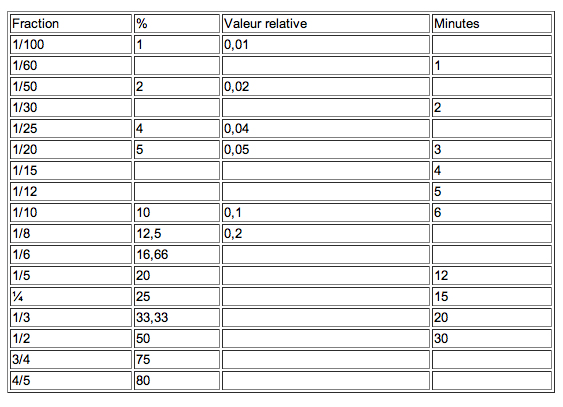
Lisez le tableau comme suit : un cinquième de X ou 1/5.X équivaut à 20% de X. ok ?
Un cinquième d'une heure équivaut à 12 minutes.
 AUTEUR : Rémi
AUTEUR : Rémi
Ancien étudiant en école de commerce, je me suis spécialisé dans les conseils pour les candidats aux admissions parallèles (tage-mage, entretien...).